• The Explanation


    The Table is a revolutionary website that allows selected elements to find bonds to create between each other.
    With such a defined idea, we would like to give a detailed discussion and explanation of how this website works.

    The Atomic Structure

    The Atomic Structure can be considered "the body" of the elements and defines their personality, what they're looking for and their attractiveness.
    Their personality and uniqueness is related to their Atomic Number, their interests are defined by their electron configuration and their attractiveness is defined by all of these variables, including their Mass Number.

    Chemistry Definition: An atom consists of a proton, a neutron, and an electron. A proton has a positive charge, a neutron has no charge/is neutral, and an electron, although a million times smaller, has a negative charge.
    The electrons are attracted by the positive charge of the protons; however they only orbit because electrons repel each other due to each having a negative charge.

    The Atomic Number

    The Atomic Number defines the metaphorical "weight" of the element; as the Atomic Number increases throughout the Table, the amount of Protons within the nucleus changes.

    Chemistry Definition: This value can't change since it is the primary "identity" of the element. If an element were to gain or lose a proton, it would change itself into a different element and event turn into an isotope.

    The Atomic Mass

    The Atomic Mass defines the "weight" of the element; as the Atomic Mass increases, this weight increases and can be considered a parallel to a person's weight.
    It does not neccessarily mean that heavier elements are less attractive (mysoginistic). For example, Hydrogen would be the lightest element in the Periodic Table.
    The Atomic Mass does not hold that much of an importance at The Table.

    Chemistry Definition: The Atomic Mass (or Mass Number) is the total amount of protons and neutrons are present within the nucleus of the element.
    The number of neutrons can be calculated by subtracting the Atomic Number from the Atomic Mass,
    since the amount of Protons are being subtracted.

    The Group

    The Group of each element represents the nationality of each element as well as their classification as a metal. Groups on the left side of the Table (including the Transition Metals) are classified as males and are metals,
    whereas the elements on the right side (from group 3 and beyond) are classified as females and are nonmetals.
    Hydrogen is an exception and is both a nonmetal and a female even though it is placed in group 1.
    Aside from being a bearer of nationality, the Group defines the amount of valence electrons an element has. The Valence Shells represent how much each element needs in order to fulfill their daily needs. For example, Chlorine would typically need one electron to complete its outer shell; meaning an element from Group 1 would definitely provide the needs of Chlorine by giving her one electron.

    Chemistry Definition: The Group of an element defines its characteristics/properties as well as the amount of electrons present in the element's valence shell. The eight different groups have their own properties.

    The Period (including the Valence Shell)

    The Period defines the amount of valence shells the elements have and in turn, these valence shells define how much an electron (or in this case, the presents given by other elements) holds its worth.
    As the amount of valence shells increase, the electrons would in time lose their worth since that specific element already holds a lot more electrons. Therefore, The Period would make the most sense defining their personality towards their privilege.

    Chemistry Definition: An element's amount of valence shells are in relation with the Period. Each element is placed in one of the seven periods. This is one of the patterns Mendeleev has been able to predict; the Periods are relative to the amount of valence shells.

    Electronegativity

    At our facilities, electronegativity defines how much an element is willing to take from another element they are willing to bond to. For elements that have a high electronegativity such as Fluorine, an electron will be taken instead of given.
    For example, Chlorine will always take from Sodium, who will always give since his electronegativity is low and Chlorine's electronegativity is high.
    In turn, this makes the likeliness of polarity increase.

    Chemistry Definition: The electronegativity of an element defines how much it is likely to pull an electron to itself. It is a given that elements in Group 7 will have high electronegativity values because their valence shells only require
    one more electron to become a full shell. However, the electronegativity value decreases as an element's Period increases. This is because the force of electronegativity slowly deteriorates as the electrons
    are located further from the nucleus; the protons' pull will slowly lose its effect as the electrons move further away from them. In an intramolecular bond, electronegativity can resolve whether a bond
    will be polar or nonpolar. Electronegativity also changes the current shape of the molecule; since electrons will be huddled together onto one atom, other atoms within the molecule will not recieve the same amount. The molecule
    turns asymmetrical.

    Polarity

    As the give-and-take values differ within molecules due to their electronegativity values, there will always be chances of polarity. Polarity is the chemical equivalent of cheating/commiting adultery.
    If an element's electronegativity has a significantly higher value compared to their bonded elements and a net positive and net negative side is created,
    there is a chance that these elements will separate and bond with other atoms going through the same process.

    Chemistry Definiton: The Polarity of a molecule is decided by a current relation between the atoms in a molecule: their electronegativity.
    As the shape of a molecule changes and turns asymmetrical, other molecules with a net positive and net negative side will be attracted to another molecule's net positive and net negative sides. However, a molecule is nonpolar if its shape is symmetrical due to each atom having a small difference between their electronegative values.

    Intermolecular Forces

    Intermolecular forces occur between molecules. There are three different types of intermolecular force: Hydrogen Bonding, Dipole-dipole, and London Dispersion. Dipole-dipole and London Dispersion are both
    classified as Van Der Waals forces.

    Hydrogen Bonding is a special type of intermolecular force that occurs when Hydrogen bonds with elements with high electronegative values: Nitrogen, Oxygen and Fluorine. Since Hydrogen only has one electron, These elements' net negative side
    will attract the net positive side of Hydrogen, even in a bond. A prime example is H2O.

    Dipole-dipole is the strongest type of intermolecular force. It occurs when a net positive side of a molecule reacts with the net negative side of another molecule. HCl is an example of this force; Hydrogen will be attracted
    to the Chlorine in a different molecule whilst Chlorine will be attracted to the Hydrogen.

    London Dispersion is the weakest type of intermolecular force. The amount of electrons essentially within an atom defines the strength of the dispersion force; the higher the amount of electrons, the stronger these Dispersion
    bonds are. Molecules that have Dispersion Forces such as Methane (CH4) freeze at low temperatures because a slight increase in temperature will directly change its state of matter.

    Intramolecular Force

    Intramolecular forces occur within molecules; they are the forces that keep atoms together. There are four main types of intramolecular forces:
    Ionic, Simple Covalent, Giant Covalent, and Metallic Bonding.

    Ionic intramolecular bonds have a direct relation to the Ionic intermolecular force; since metals and nonmetals bond within an Ionic intramolecular force, the electronegativity will usually differ a lot. Therefore, this force can be hollistically viewed as a positive element giving its electrons to a negative element.
    Once this intramolecular force is created, the Ionic intermolecular force allows one side of this molecule to gain a net negative charge and consequently, the opposite side gains a net positive charge. The molecule can then bond with other molecules through this intermolecular force.

    Simple Covalent structures are a smaller, weaker type of bond that occurs between nonmetals. This intramolecular force is related to the London Dispersion force; two nonmetals bond together. Since these two nonmetals will, more or less, have little difference between their electronegativity values, Dipole-dipole will not occur (with Hydrogen as an exception). These bonds typically have low melting and boiling points, partly because the intermolecular bonds in effect
    (Dipole-dipole) are weak as is.

    Giant covalent structures are made out of many various nonmetals that, as the amount of electrons increase, the intermolecular and intramolecular forces become stronger. Therefore, the melting and boiling point increases exponentially.

    Metallic bonding is an intramolecular force that occurs between metals. In a metallic bond, the atoms' electrons are free to move around the protons. These intramolecular bonds are typically very strong; these structures' melting and boiling points are high. Metallic bonding has its very own type of intermolecular force, primarily due to its unique type of sharing.

    This Website is Sponsored By:

    The Cathode Ray Tube

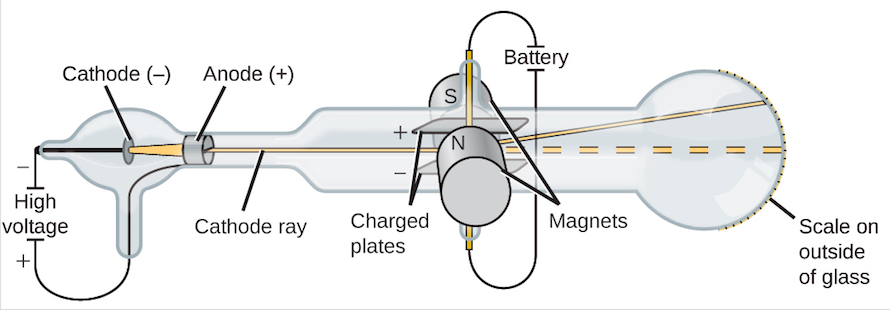
    Courtesy of: Khan Academy


    The Cathode Ray Tube essentially helped discover the negatively charged electrons. Using a device (see diagram) that was able to create a beam and deflect it,
    J.J. Thompson was the first to learn about "smaller particles" present within an atom.
    A cathode and anode (made of metal) was placed within a modified test-tube setup, along with magnets with opposite charges along the sides and two more metal
    plates that were connected to a power source, both also with opposite charges. On the other end of the tube, a special type of film is placed; this film is hit by the cathode ray and defines whether the ray is deflected or not.

    In this specific device, when the cathode ray was created, the film at the end showed that when the cathode particles were initiated, they deflected unto the side of the film next to the positive metal plate. J.J. Thompson then concluded that there are particles within these cathode rays that were attracted to protons and that they existed within the atoms. This proved that electrons existed, and that the plum pudding model had to be refined, or ultimately changed ("Discovery of the electron and the nucleus ", Khan Academy).

    Bibliography

    "Does an Atoms Mass Number or Atomic Number Ever Change? | Socratic." Socratic.org, Socratic, socratic.org/questions/does-an-atoms-mass-number-or-atomic-number-ever-change.

    "Intramolecular and Intermolecular Forces." Khan Academy, Khan Academy, www.khanacademy.org/test-prep/mcat/chemical-processes/covalent-bonds/a/intramolecular-and-intermolecular-forces.

    "GCSE Bitesize: Atomic Structure." BBC, BBC, www.bbc.co.uk/schools/gcsebitesize/science/add_ocr_gateway/periodic_table/atomstrucrev1.shtml.

    "Discovery of the Electron and Nucleus." Khan Academy, Khan Academy, www.khanacademy.org/science/chemistry/electronic-structure-of-atoms/history-of-atomic-structure/a/discovery-of-the-electron-and-nucleus.

    "GCSE Bitesize: Covalent Bonding - Giant Covalent Structures." BBC, BBC, www.bbc.co.uk/schools/gcsebitesize/science/add_aqa_pre_2011/atomic/differentsubrev3.shtml.